redis-zskiplist源码阅读

zskiplist结构

/*
 * 跳跃表
 */
typedef struct zskiplist {

    // 表头节点和表尾节点
    struct zskiplistNode *header, *tail;

    // 表中节点的数量
    unsigned long length;

    // 表中层数最大的节点的层数
    int level;

} zskiplist;

/*
 * 跳跃表节点
 */
typedef struct zskiplistNode {

    // 成员对象
    robj *obj;

    // 分值
    double score;

    // 后退指针
    struct zskiplistNode *backward;

    // 层 , 柔性数组
    struct zskiplistLevel {

        // 前进指针
        struct zskiplistNode *forward;

        // 跨度
        unsigned int span;

    } level[];

} zskiplistNode;

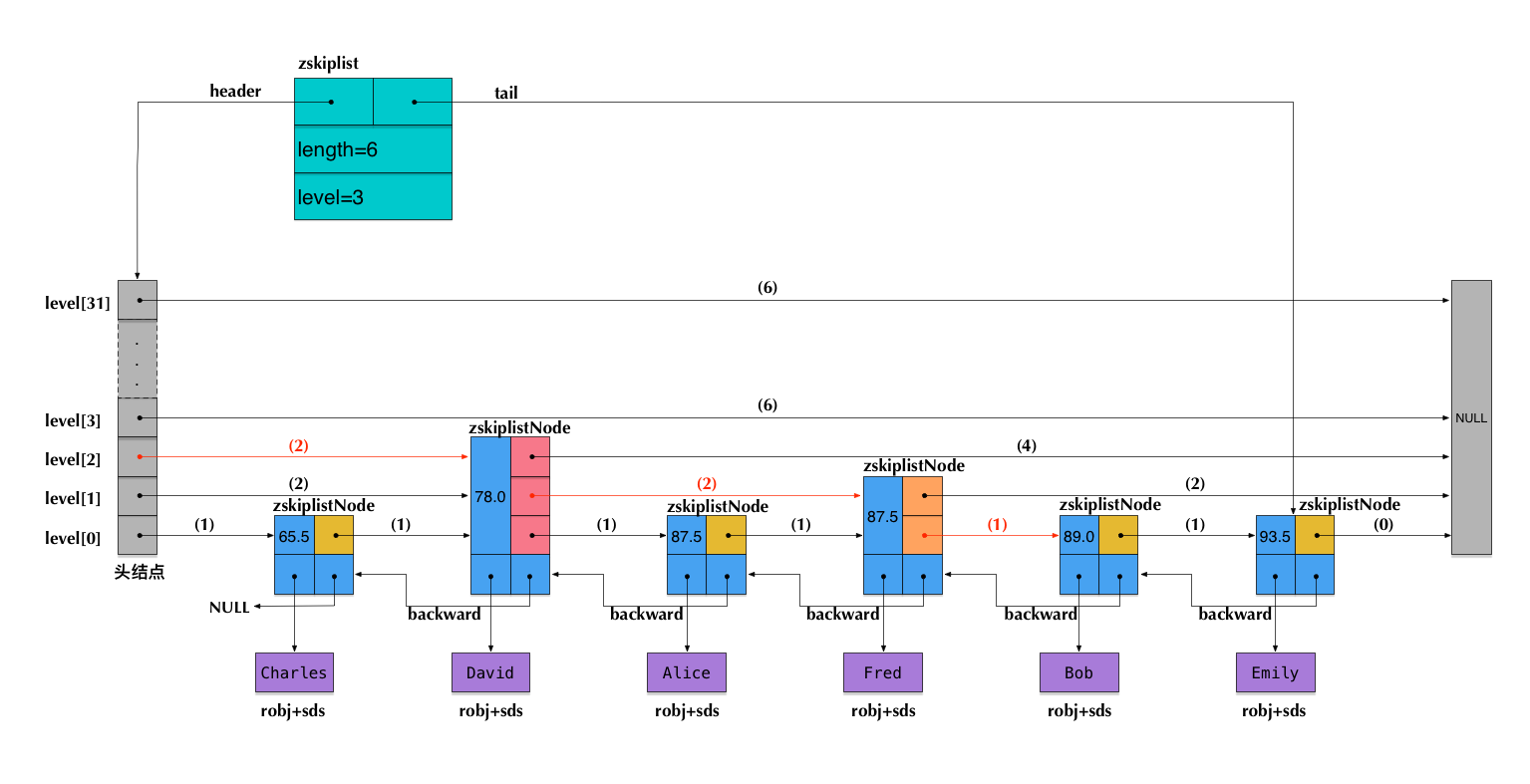
什么是span,forward,score,rank

1. span是指同一层的当前节点到下一个节点相隔的节点数，比如说，在L3这一层上，header的span为2，因为他在L3的下一个节点是node2
2. forward指的是同一层上，当前节点指向下一个节点的指针
3. score就是设置的一个分值，用来做排序的
4. rank是指当前节点到头节点的节点数目，比如说L3的node2的rank值为2

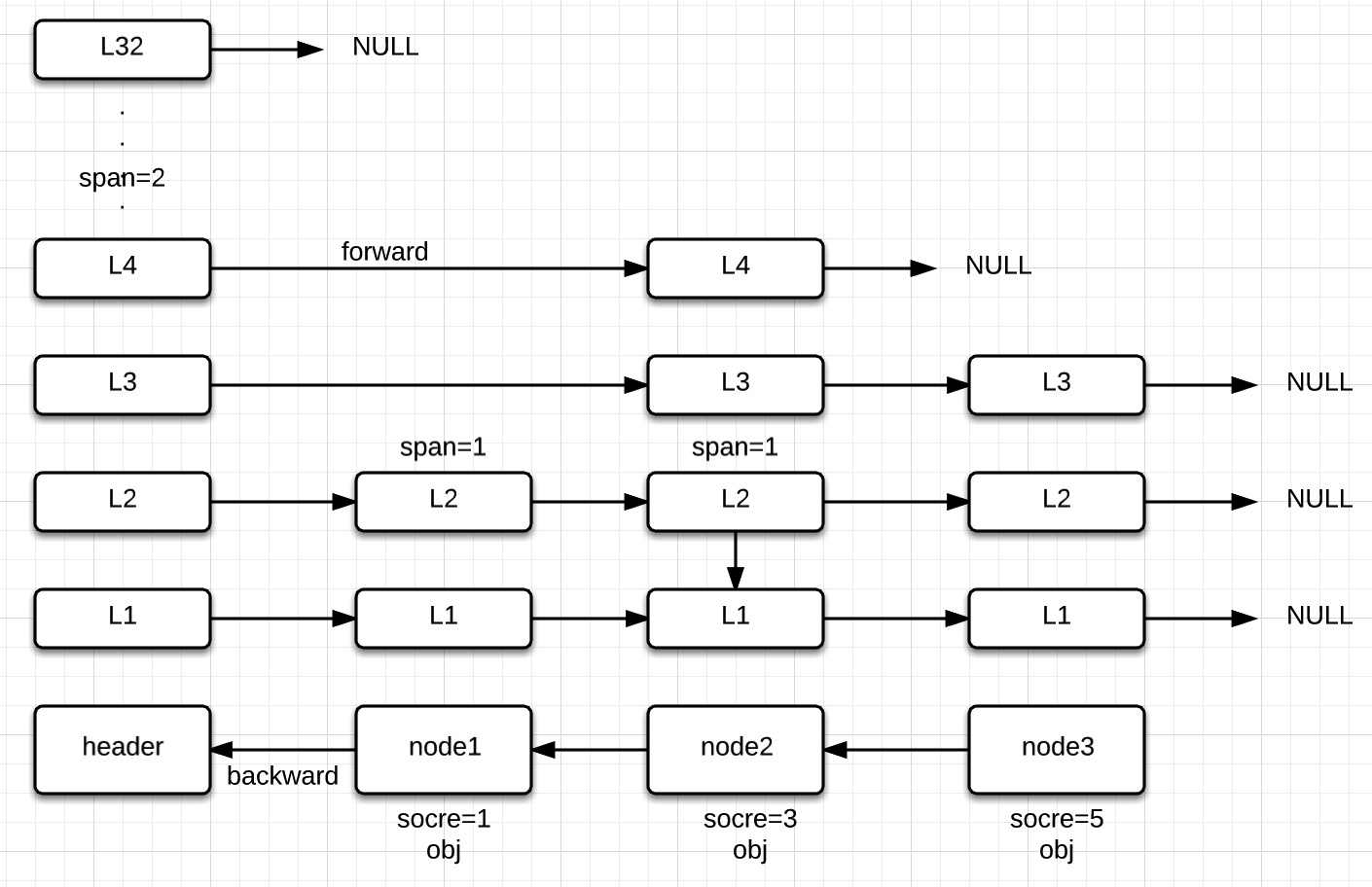
插入节点

1. 判断随机的lever是否比目前的最大lever要大，如果大，需要先将大于最大的level的部分进行初始化
2. 寻找到同一层当前节点的score比插入节点的score小，下一个节点的score比插入score大的节点
3. 将节点的forward指针替换
4. 计算span值（这个很有意思）

5. span计算核心代码及事例（如下）

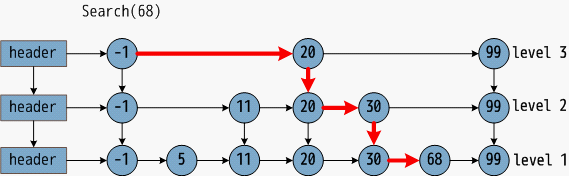
   如下图：假设zskiplist的节点已经存在：-1，5，11，30，68，99，现在插入20这个节点，计算他的span的过程

   1. 目前的zsl->lever为3，当前的x节点是header，在一个for循环中，由于i=zsl->lever-1,故rank[2]=0
   2. 由于x的下一个节点的score是-1，小于即将插入的score为20这个值，故：rank[i] += x->level[i].span；rank[2]=1;x->level[2].span=1（level3上x也就是header节点的下一个节点（score为-1的节点）的距离为1）,x节点替换成score为-1所在的节点
   3. 由于当前的i为1不等于zsl->lever-1=2,故rank[1]=rank[2]=1
   4. x的下一个节点的score是11，小于即将插入的score为20的这个值，故：rank[i] += x->level[i].span;rank[1]为3;即：x->lever[1].span+rank[1]; x->lever[1].span=2（score为-1的节点到score为11的节点的距离为2）；rank[1]=1;x节点替换为score为11的节点
   5. 同理可得，rank[0]=3;
   6. 截止到此处，rank数组已经获取到了：rank[0]=3;rank[1]=3;rank[2]=1;
   7. 接下来对于score为20的节点的span的计算与它的前一个节点的计算就看下面两行代码：
   8. x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]);
   9. update[i]->level[i].span = (rank[0] - rank[i]) + 1;

for (i = zsl->level - 1; i >= 0; i--) {//按层遍历，最高层开始遍历，最底层遍历的话要走过每一个节点，跳跃表就没有任何意义了

        /* store rank that is crossed to reach the insert position */
        // 如果 i 不是 zsl->level-1 层
        // 那么 i 层的起始 rank 值为 i+1 层的 rank 值
        // 各个层的 rank 值一层层累积
        // 最终 rank[0] 的值加一就是新节点的前置节点的排位
        // rank[0] 会在后面成为计算 span 值和 rank 值的基础
        rank[i] = i == (zsl->level - 1) ? 0 : rank[i + 1];//进行跳跃，如果最上面一层，老实的初始化，如果到了倒数第二层，则以最上面一层为起点开始寻找

        redisLog(REDIS_WARNING, "rank[%d]:%d", i, rank[i]);
        redisLog(REDIS_WARNING, "x->score:%f", x->score);
        // 沿着前进指针遍历跳跃表
        // T_wrost = O(N^2), T_avg = O(N log N)
        /*
          同一层往前寻找，直到不再满足以下条件再找下一层，
          将要和新节点相连接的节点满足如下条件：
            1、forward不存在
            2、forward节点的score大于新节点的score
            3、forward的节点和新的节点的score相等，forward节点的值大于新节点
         */
        if (x->level[i].forward) {
            redisLog(REDIS_WARNING, "判断的：x->level[%d].forward->score:%f", i, x->level[i].forward->score);
        }
        while (x->level[i].forward &&
               (x->level[i].forward->score < score ||
                // 比对分值
                (x->level[i].forward->score == score &&
                 // 比对成员， T = O(N)
                 compareStringObjects(x->level[i].forward->obj, obj) < 0))) {

            // 记录沿途跨越了多少个节点
            redisLog(REDIS_WARNING, "循环中的：x->level[%d].forward->score:%f", i, x->level[i].forward->score);
            rank[i] += x->level[i].span;

            // 移动至下一指针
            x = x->level[i].forward;
            redisLog(REDIS_WARNING, "rank[%d]值:%d", i, rank[i]);
        }
        // 记录将要和新节点相连接的节点
        update[i] = x;
        redisLog(REDIS_WARNING, "score:%f", score);
        redisLog(REDIS_WARNING, "第%d遍历结束", i);
    }

for (i = 0; i < level; i++) {
    // 设置新节点的 forward 指针
    x->level[i].forward = update[i]->level[i].forward;

    // 将沿途记录的各个节点的 forward 指针指向新节点
    update[i]->level[i].forward = x;

    /* update span covered by update[i] as x is inserted here */
    // 计算新节点跨越的节点数量
    x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]);
    redisLog(REDIS_WARNING, "update[%d]->score：%f",  i, update[i]->score);
    // 更新新节点插入之后，沿途节点的 span 值
    // 其中的 +1 计算的是新节点
    update[i]->level[i].span = (rank[0] - rank[i]) + 1;

    redisLog(REDIS_WARNING, "新节点的span[%d]：%d", i, update[i]->level[i].span);
}            

zskiplistNode *zslInsert(zskiplist *zsl, double score, robj *obj) {
    zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
    unsigned int rank[ZSKIPLIST_MAXLEVEL];
    int i, level;

    redisAssert(!isnan(score));

    // 总体思路是先查找记录每层的节点位置,然后走和链表一样的插入操作
    // 在各个层查找节点的插入位置, 更新update
    // T_wrost = O(N^2), T_avg = O(N log N)
    x = zsl->header;
    redisLog(REDIS_WARNING, "lever值为：%d", zsl->level);
    redisLog(REDIS_WARNING, "key为：%s", obj->ptr);
    for (i = zsl->level - 1; i >= 0; i--) {//按层遍历，最高层开始遍历，最底层遍历的话要走过每一个节点，跳跃表就没有任何意义了

        /* store rank that is crossed to reach the insert position */
        // 如果 i 不是 zsl->level-1 层
        // 那么 i 层的起始 rank 值为 i+1 层的 rank 值
        // 各个层的 rank 值一层层累积
        // 最终 rank[0] 的值加一就是新节点的前置节点的排位
        // rank[0] 会在后面成为计算 span 值和 rank 值的基础
        rank[i] = i == (zsl->level - 1) ? 0 : rank[i + 1];//进行跳跃，如果最上面一层，老实的初始化，如果到了倒数第二层，则以最上面一层为起点开始寻找，如图的L2的20这个节点，他的初始的rank是4而不是0，如果是0的话，因此他的路线才是l3的20节点，再从l2的20去找，而不是l2的-1节点重新遍历

        redisLog(REDIS_WARNING, "rank[i+1]:%d", rank[i + 1]);
        // 沿着前进指针遍历跳跃表
        // T_wrost = O(N^2), T_avg = O(N log N)
        /*
          同一层往前寻找，直到不再满足以下条件再找下一层，
          将要和新节点相连接的节点满足如下条件：
            1、forward不存在
            2、forward节点的score大于新节点的score
            3、forward的节点和新的节点的score相等，forward节点的值大于新节点
         */
        while (x->level[i].forward &&
            (x->level[i].forward->score < score ||
                // 比对分值
                (x->level[i].forward->score == score &&
                // 比对成员， T = O(N)
                compareStringObjects(x->level[i].forward->obj, obj) < 0))) {

            // 记录沿途跨越了多少个节点
            rank[i] += x->level[i].span;//将小于自己的节点的span值加起来，例如：rank[1]的值为rank[0]的值（也就是l3的-1节点的span加上l3的20节点的span）加上下一个节点的span（l2的30节点的span值）

            // 移动至下一指针
            x = x->level[i].forward;
            redisLog(REDIS_WARNING, "rank值:%d", rank[i]);
        }
        // 记录将要和新节点相连接的节点
        update[i] = x;
        redisLog(REDIS_WARNING, "span的值：%d", rank[i]);
        redisLog(REDIS_WARNING, "第%d个指针", i);
        redisLog(REDIS_WARNING, "score:%f", score);
    }

    /* we assume the key is not already inside, since we allow duplicated
     * scores, and the re-insertion of score and redis object should never
     * happen since the caller of zslInsert() should test in the hash table
     * if the element is already inside or not. 
     *
     * zslInsert() 的调用者会确保同分值且同成员的元素不会出现，
     * 所以这里不需要进一步进行检查，可以直接创建新元素。
     */

    // 获取一个随机值作为新节点的层数
    // T = O(N)
    level = zslRandomLevel();

    // 如果新节点的层数比表中其他节点的层数都要大
    // 那么初始化表头节点中未使用的层，并将它们记录到 update 数组中
    // 将来也指向新节点
    redisLog(REDIS_WARNING, "随机分配的level:%d", level);
    if (level > zsl->level) {

        // 初始化未使用层（因为是初始化大于最高层的层，因此只有header节点指向这些层）
        // T = O(1)
        for (i = zsl->level; i < level; i++) {
            rank[i] = 0;
            update[i] = zsl->header;
            update[i]->level[i].span = zsl->length;
        }

        // 更新表中节点最大层数
        zsl->level = level;
    }

    // 创建新节点（创建数据和score）
    x = zslCreateNode(level, score, obj);

    // 分别处理每层update中对应的链表的insert操作
    // 将前面记录的指针指向新节点，并做相应的设置
    // T = O(1)
    for (i = 0; i < level; i++) {

        // 设置新节点的 forward 指针
        x->level[i].forward = update[i]->level[i].forward;

        // 将沿途记录的各个节点的 forward 指针指向新节点
        update[i]->level[i].forward = x;

        /* update span covered by update[i] as x is inserted here */
        // 计算新节点跨越的节点数量
        x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]);

        // 更新新节点插入之后，沿途节点的 span 值
        // 其中的 +1 计算的是新节点
        update[i]->level[i].span = (rank[0] - rank[i]) + 1;
        redisLog(REDIS_WARNING, "新节点的span：%d", x->level[i].span);
    }

    /* increment span for untouched levels */
    // 未接触的节点的 span 值也需要增一，这些节点直接从表头指向新节点
    // T = O(1)
    for (i = level; i < zsl->level; i++) {
        update[i]->level[i].span++;
    }

    // 设置新节点的后退指针
    x->backward = (update[0] == zsl->header) ? NULL : update[0];
    if (x->level[0].forward) {
        x->level[0].forward->backward = x;
    }
    else {
        zsl->tail = x;
    }

    // 跳跃表的节点计数增一
    zsl->length++;

    redisLog(REDIS_WARNING, "长度:%lu", zsl->length);
    printf("\n");
    return x;
}

节点删除

1. 找出要删除节点的前一个节点，存入update中，再遍历
2. 如果删除的节点不存在当前层，则span-1（因为需要删除当前节点）
3. 如果要删除的节点存在当前层，则span为当前节点的span+删除节点的span-1
4. 判断最大的level值，替换前置，后置指针，及length值

int zslDelete(zskiplist *zsl, double score, robj *obj) {
    zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
    int i;

    // 查找目标节点, 把前置节点记录在update中
    // 遍历跳跃表，查找目标节点，并记录所有沿途节点
    // T_wrost = O(N^2), T_avg = O(N log N)
    x = zsl->header;
    for (i = zsl->level-1; i >= 0; i--) {

        // 遍历跳跃表的复杂度为 T_wrost = O(N), T_avg = O(log N)
        while (x->level[i].forward &&
            (x->level[i].forward->score < score ||
                // 比对分值
                (x->level[i].forward->score == score &&
                // 比对对象，T = O(N)
                compareStringObjects(x->level[i].forward->obj, obj) < 0))) {

            // 沿着前进指针移动
            x = x->level[i].forward;
        }

        // 记录沿途节点
        update[i] = x;
    }

    /* We may have multiple elements with the same score, what we need
     * is to find the element with both the right score and object. 
     *
     * 检查找到的元素 x ，只有在它的分值和对象都相同时，才将它删除。
     */
    x = x->level[0].forward;
    if (x && score == x->score && equalStringObjects(x->obj, obj)) {
        // T = O(1)
        zslDeleteNode(zsl, x, update);
        // T = O(1)
        zslFreeNode(x);
        return 1;
    } else {
        return 0; /* not found */
    }

    return 0; /* not found */
}

/**
 * zskiplistNode *x 删除节点的指针
 * zskiplistNode **update 删除节点的backward节点的指针
 */
void zslDeleteNode(zskiplist *zsl, zskiplistNode *x, zskiplistNode **update) {
    int i;

    // 更新所有和被删除节点 x 有关的节点的指针，解除它们之间的关系
    // T = O(1)
    for (i = 0; i < zsl->level; i++) {
        //要删除的节点存在当前层
        if (update[i]->level[i].forward == x) {
            update[i]->level[i].span += x->level[i].span - 1;
            update[i]->level[i].forward = x->level[i].forward;
        } else {//删除的节点不存在当前层
            update[i]->level[i].span -= 1;
        }
    }

    // 更新被删除节点 x 的前进和后退指针
    if (x->level[0].forward) {
        x->level[0].forward->backward = x->backward;
    } else {
        zsl->tail = x->backward;
    }

    // 更新跳跃表最大层数（只在被删除节点是跳跃表中最高的节点时才执行）
    // T = O(1)
    while(zsl->level > 1 && zsl->header->level[zsl->level-1].forward == NULL) {
        zsl->level--;
    }

    // 跳跃表节点计数器减一
    zsl->length--;
}

按照分值范围删除

1. 找到删除范围的最小的score的前一个节点的指针存入update
2. 在第0层中，找到所有的要删除的节点，并依次删除
3. 需要注意的是x->level[0].forward一定是删除范围最小的score的前一个最靠近的节点（因为第0层中是存在所有的节点的）
4. 另外关注一点的的：删除是从小到大，依次删除的，这样能保证update中的值，一定是被删除节点的前一个节点，比如说现在存在score为：1，2，3，4，5，6，7的节点，我要删除2-6之间的节点，那么我依次删除3，4，5；第一次删除3的时候他的前置节点是2，第二次删除4的时候，他的前置节点也是2，因为3被删除了

unsigned long zslDeleteRangeByScore(zskiplist *zsl, zrangespec *range, dict *dict) {
    zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
    unsigned long removed = 0;
    int i;

    // 记录所有和被删除节点（们）有关的节点
    // T_wrost = O(N) , T_avg = O(log N)
    x = zsl->header;
    for (i = zsl->level-1; i >= 0; i--) {
        while (x->level[i].forward && (range->minex ?
            x->level[i].forward->score <= range->min :
            x->level[i].forward->score < range->min)) {
                x = x->level[i].forward;
        }
        update[i] = x;
    }

    /* Current node is the last with score < or <= min. */
    // 定位到给定范围开始的第一个节点
    x = x->level[0].forward;

    /* Delete nodes while in range. */
    // 删除范围中的所有节点
    // T = O(N)
    //在第0层中，找到所有的要删除的节点，并依次删除
    while (x &&
           (range->maxex ? x->score < range->max : x->score <= range->max))
    {
        // 记录下个节点的指针
        zskiplistNode *next = x->level[0].forward;
        zslDeleteNode(zsl, x, update);
        dictDelete(dict, x->obj);
        zslFreeNode(x);
        removed++;
        x = next;
    }
    return removed;
}